“Altın Oran” teknolojide, tedavide, bilimde ve hayatın diğer birçok alanında kullanılabilir mi? Şeklin ötesinde, her bir bilgi sisteminin mantık yapılarına uyarlanabilir mi?
Otomotiv sektöründe kullanılmaya çalışıldığı ortadadır ama bu “Güzelliğin Altın Oranı” hayatımızın ve tüm yapıların içerisine yayılamaz mı? Tarihe baktığımızda sanat ve mimaride kullanıldığını görüyoruz. Matematiğin bu güzellikler oranını, hayatımızın her alanını güzelliklerle donatmaya hazır görünüyor.
İnsanoğlu tarihinde de bugün olduğu gibi hep bir şeyleri merak etmiştir. Akla gelen sorulardan bir tanesi de “parça ile bütünü arasındaki en hoş uyum nasıl sağlanabilir?” sorusudur. Örneğin: bir doğru nasıl bölünmeli ki ortaya çıkan iki parça her durumda birbiri ile özel bir oranda olsun. “Doğru parçası” birçok şekilde ikiye ayrılabilir. Hangi ayrımda bu özel oran bulunabilir ve bu oran acaba dünyamıza ve vücutlarımıza ne kadar hakim?
Altın Oran
PHI (Altın Oran); Φ = CB / AC = AB / CB = 1.618034 = 1+√5 / 2
Peki bu oran niçin bu kadar önemli? Çünkü başta vücudumuz olmak üzere bir çok yerde karşımıza çıkıyor ve bizim hoşlanma duygumuzu yönetiyor. Göze en hoş gelen uyumdur altın oran. Göz nizamının oranıdır. Parçaların ve bütünlerin ahenk şeklinde oluşudur. Altın oran bizim ve dünyamızın güzelliğinin matematiksel karşılığıdır. Altın oran bir güzellik oranıdır.
Tarihe baktığımızda ilk olarak ünlü mısır piramidi “keops”ta bu oranı görüyoruz. Piramitlerde “PI” oranı ile birlikte “PHI” yani altın oranı da görüyoruz. Euclid “elementler” tezinde bir doğrunun 0,618 oranında bölündüğü takdirde önemli bir ayırma yapılabileceğinden bahsetmektedir. Parthenon Tapınağında ise altın oran kendisini yunan mimarisinde açıkça gösterir. Matematikte ilk olarak İtalyan matematikçi Leonardo Fibonacci kendi adıyla anılan “Fibonacci serisinde” bu oranı keşfetmiştir.
Leonardo Da Vinci “beş platonik cisim” adlı resimlerinde bu oranı göstermiş ve “Son Akşam Yemeği” adlı ünlü tablosunda İsa ve havarilerinin oturduğu yemek masasının boyutlarında ve arka duvar ve pencerelerde bu oranı kullanmıştır. “Mona Lisa” tablosunun boyunun enine oranı altın oranı verir. “Aziz Jerome” tablosunda yine Da Vinci boy – en oranında altın oranı kullanmıştır. Picasso da yine bu oranı kullananlardandır.Rönesans sanatçıları bu oranı biliyor ve eserlerinde denge ve güzelliğin oluşumu için kullanıyorlardı. Roger Penrose, imkansız olduğu düşünülen “yüzeylerin beşli simetriye göre katlanmasını” bu oran sayesinde bulabilmiştir. Ünlü mimarımız “Mimar Sinan” da bu oranı bir çok eserinde kullanmıştır. Özellikle “Süleymaniye” ve “Selimiye” camilerinin minarelerinde bu oran görülmektedir.
Soru şudur: Eğer bir çift tavşan her ay yeni bir çift tavşan doğurursa ve her yeni tavşan çifti kendi doğumlarından iki ay sonra yavrulamaya başlarsa, bir çift tavşandan bir yılda kaç çift tavşan üretilebilir? Tabi tavşanların aynı cins olup olmaması yada bazı tavşanların ölmesi yada vahşi hayvanlar tarafından yenmeleri gibi ihtimalleri yok sayıyoruz.
Bu sorunun matematiksel açılımı bize şu seriyi verir: 1,1,2,3,5,8,13,21,34,55,89,144
Bu serinin ifadesi ise şöyledir: İlk ikisi dışında her sayı kendisinden önce gelen iki sayının toplamından oluşur. Bu dizi sonsuza dek bu şekilde sürdürülebilir. T1 , T2 , T3 , T4 , T5 , T6 , T7,…….Tn. ( T = Tavşan ) Tn kendinden önce gelen Tn-2 ve Tn-1 sayılarının toplamıdır. Böylece sonsuz bir sayı dizisi tanımlayabiliriz. Tn= (Tn-1) + (Tn-2) Bu formülle tanımlanan tüm n’ler de sonsuza gidilebilir. T1 ve T2 nin 1 olduğunu göz ardı etmeden tabi.
Serideki oranlara baktığımızda ise:
1) 1.000000
2) 0.500000
3) 0.666666
4) 0.600000
5) 0.625000
6) 0.615385
7) 0.619048
8) 0.617647
9) 0.618182
10) 0.617978
11) 0.618056
12) 0.618026
13) 0.618037
14) 0.618033
15) 0.618034 = Φ ( Altın Oran )
16) 0.618034 = Φ ( Altın Oran )
Altın orana ulaşırız.
Fibonacci sayıları niçin ilgi çekicidir?
Sayı dizisi doğada bir çok yerde karşımıza çıkar. Bitkilerin dal ve yaprak serilerinden hayvanların vücutlarındaki oranlara kadar. Papatyalarda bu yaprak sayılarında görünür. Papatya taç yaprak sayısı: 21, 34, 55 ve 89 dur. Bunlarda yine Fibonacci serisidir.
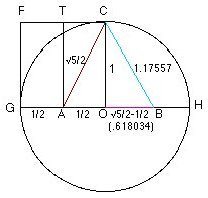
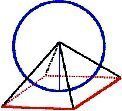
Çember üzerinde OC yarıçapı 1 kabul edildiğinde ve FCOG karesi oluşturulduğunda ve FC kenarının orta noktasına olan T den GO kenarına bir dikme inip oluşan TCAO dikdörtgeninin köşegenini (AC) bir ikizkenar üçgenin (ABC) kenarlarından biri olduğunu kabul ettiğimizde OB kenarı bize Altın Oranı verir. OCB açısı 31″43’ve OBC açısıda 58″17’olarak bulunur.
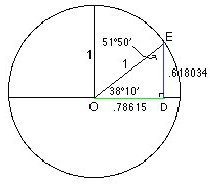
Yine çember üzerinde yandaki gibi bir üçgen oluşturulduğunda bu sefer hipotenüs 1 kabul edilir ve ED uzunluğu (0.618034) OD kenar uzunluğuna (0.78615) bölünürse sonuç OD kenarının uzunluğuna (0.78615) eşit çıkmaktadır. OD kenar uzunluğu 4 ile çarpıldığında ise 3,1446 olur ki bu Pİ sayısına çok yakındır. 38″10’açıya sahip bir dik üçgenin Pİ oranı ile Altın Oranın çok özel ve ilginç bir bütünleşmesidir.
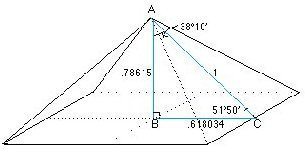
Büyük Piramit
Kadim mısır uygarlığı bu oranları nereden biliyordu? Keops piramidi 38″10’lık bir üçgeni oluşturacak biçimde inşa edilmiştir. Yüzey eğimi 51″50’lık bir açıdır. Piramidin gerçek ölçüleri şunlardır: AB=146.6088m BC=115.1839m AC=186.3852m’dir. BC kenar uzunluğunun yarısıdır. Çevre uzunluğu BC x 8 dir. 0.618034 x 8 = 4.9443 Piramidin yüksekliği0.78615 inbir çemberin yarıçapı olduğu kabul edildiğinde bu çemberin uzunluğu (çevresi) yine 4.9443 olacaktır. Şu sonuca varılır: Büyük Piramit, yatay düzlemde sahip olduğu çevre uzunluğunun aynısına düşey düzlemde daire olarak ta sahiptir.
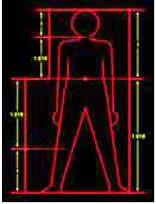
İnsan vücudunda altın oran
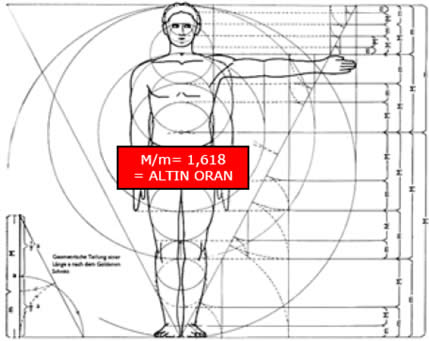
Göbek ile ayak arasındaki uzaklık 1 birim kabul edilirse insanın boyu 1,618 e denk gelir.
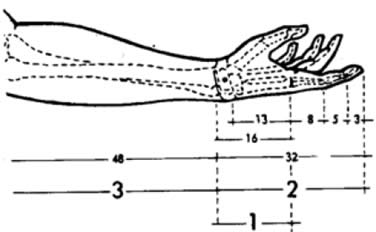
Parmak ucu-dirsek arası / El bileği-dirsek arası,
Omuz hizasından baş ucuna olan mesafe / Kafa boyu,
Göbek-baş ucu arası mesafe / Omuz hizasından baş ucuna olan mesafe,
Göbek-diz arası / Diz-ayak ucu arası. Oranları yine Altın Oranı verir.
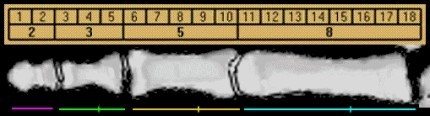
Ellerimizde de yine aynı oran karşımıza çıkar. 2 elimizin 3er bölümden oluşan parmakları ve her bir elimizde 5 parmağımız vardır. Sadece 8 parmağımızda üçer boğum vardır. 2 – 3 – 5 – 8 dizilimi Fibonacci dizilimine uygundur.
DNA moleküllerimizde de bu oran vardır. DNA molekülü iç içe 2 sarmaldan oluşur ve bu sarmalların uzunluğu 34 angström ve genişliği 21 angström’dür. 21 ve 34 sayıları ardışık Fibonacci sayılarıdır.
İnsan kafasını incelediğimizde bir altın dikdörtgenin içerisinde olduğu görülür. Kulaklar arası mesafe, gözle üst dudak arası mesafe, burnun altı ile çene arasındaki mesafe bu orandadır. Bu şüphesiz mili metrik bir yaklaşım değildir ama bu orana yaklaşıldıkça insanların daha güzel ve yakışıklı bulunduğunu söyleyebiliriz.
Altın Dikdörtgen
Orana göre çizilmiş bu dikdörtgen ile parmaklarımız arasında bir benzerlik bulunmaktadır.
Bitkilerde altın oran
Ayçiçeğinde saat yönünde 55 ve zıt yönde 89 ayçekirdeği bulunur.
89 / 55 = 1,618
Papatyalar Fibonacci serisi üzere gelişir.
Çam kozalağında, kozalağın altındaki ve üstündeki sabit noktalar arasında bir spiral vardır. Bu spiralin eğrilik açısı Altın Oran’dır.
Tütün bitkisinin yapraklarının dizilişindeki eğriliğin tanjantı Altın Oranı verir.
Aynı biçimde eğrelti otlarında da bu oran göze çarpmaktadır.
Hayvanlar
Deniz kabuklarındaki eğriliğin (spiral) tanjantı yine Altın Oranı verir.Salyangoz kabuğu eğer bir düzleme aktarılırsa bu düzlem altın dikdörtgeni oluşturur.
Uzay
Bilim adamlarının ulaştığı sonuca göre evrenin şekli bir dodecahedrondur (12 yüzü eşkenar beşgenlerden ) Buda bize evrenin şeklinde de PHI sayısının yani Altın Oranın olduğunu gösterir.
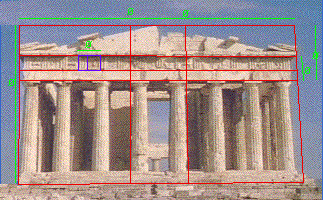
Parthenon Tapınağı
Sonuç: Kuşkusuz örnekler bunlarla sınırlı değildir. Hayvanlar aleminde, bitkiler aleminde ve insan vücudunun kendisinde ve uzayın derinliklerinde, spiral galaksilerin içeriğinde bile bu oran vardır ve bilinmektedir. Her şeyin en temel oranı ve mutlak sabit olarak ta görülmemelidir Altın Oran. Önemli ve bir çok yerde karşımıza çıkan bir orandır. İnsan yapısı olmayan ve yine insanlar tarafından güzel olarak değerlendirilen çoğu yapıda bulunur. İnsanlarında kendi üretimlerinde doğa ile tam bir uyum sergilemesi ve doğadan aldığı güzelliği yine doğanın güzelliğin içine yerleştirdiği matematik ile mümkündür. Matematik güzeldir. Matematik insanın ruhunun güzelliğinin sayısal ifadesidir. Matematik çok güzeldir.
